Frequently Asked Questions (FAQs)
- What are orbital elements?
- I'm teaching a course on the solar system. Can you help?
- I'd like to publish information from your site on my site. Do I need permission?
- Do you have equations for computing approximate positions of the planets?
- I want to write my own solar system "calculator". Where do I find the relevant equations?
- How do I find out where my favorite planet is going to be at some specified time?
- Do you provide star-charts, star coordinates, or other stellar data?
- What is an astronomical unit (au)?
- What is the time scale used for the solar system ephemerides?
- What's the exact value of... <insert your favorite orbital element here>?
- What about planet X?
What are orbital elements?
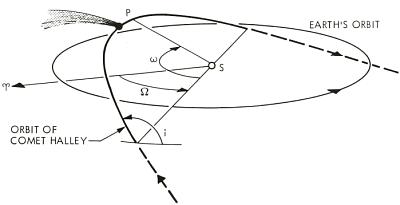
Orbital elements describe a conic (most commonly an ellipse) in inertial space. They also describe an object’s state (equivalent to its Cartesian position and velocity) at a specific epoch. Typically orbital elements are used to express an object’s osculating orbit (an orbit tangent to and approximating the actual orbit) at the specified epoch. On this site, we use both Keplerian elements and so-called comet elements.
Keplerian elements are eccentricity, semimajor axis, mean anomaly, inclination, longitude of the ascending node, and argument of perihelion. In some cases, longitude of perihelion is used instead of the argument of perihelion. Comet elements are eccentricity, perihelion distance, time of perihelion passage, inclination, longitude of the ascending node, and argument of perihelion.
Osculating orbital elements are often used in two-body propagation to estimate the state (position and velocity) of a body at some time other than the epoch. It is important to realize that for some bodies, especially planetary satellites and comets, that such estimates may be grossly in error with respect to the actual orbit. In general, the farther away in time from the epoch, the greater the error.
A complete description of orbital elements and their use in celestial mechanics is beyond the scope of this web site. More information can be found in a number of texts. See the FAQ entry below for some relevant books.
I'm teaching a course on the solar system. Can you help?
I'd like to publish information from your site on my site. Do I need permission?
Most of the content on our site is covered under JPL's copyright statement (toward the bottom of the page). It is also important to understand that use of information from our site does not in any way imply endorsement of that end use.
Do you have equations for computing approximate positions of the planets?
I want to write my own solar system "calculator". Where do I find the relevant equations?
The following books provide fundamental equations used in celestial mechanics.
- “Explanatory Supplement to the Astronomical Almanac”, ed. P. K. Seidelmann, 1992, University Science Books.
- “Fundamentals of Astrodynamics”, R.R. Bate, D.D. Mueller, J.E. White, 1971, Dover Publications, Inc.
- “Fundamentals of Celestial Mechanics”, J.M.A. Danby, 1992, Willmann-Bell.
- “Methods of Orbit Determination for the Micro Computer”, D. Boulet, 1991, Willmann-Bell.
- “Orbital Mechanics”, J.E. Prussing, B.A. Conway, 1993, Oxford University Press.
- “Orbits for Amateurs with a Microcomputer”, D. Tattersfield, 1984, Halsted Press.
- “Spherical Astronomy”, R. M. Green, 1985, Cambridge University Press.
- “Vectorial Astrometry”, C.A. Murray, 1983, Adam Hilger Ltd.
The above list is not necessarily complete nor intended to imply any endorsement by JPL or Caltech.
How do I find out where my favorite planet is going to be at some specified time?
Do you provide star-charts, star coordinates, or other stellar data?
What is an astronomical unit (au)?
The astronomical unit was redefined as a unit of length exactly equal to 149,597,870,700 meters during the August 2012 General Assembly of the International Astronomical Union (IAU). The astronomical unit, now denoted with lower case letters (au), is a convenient unit of measure for distance in the Solar System being approximately equal to the average Sun-Earth distance. The average Sun-Earth distance is not an exact quantity because the orbit of the Earth about the Sun is not exactly elliptical due to changing perturbations by other planets and because general relativity slightly modifies the elliptical solutions obtained from Newton's theory of gravity.
Prior to 2012, the astronomical unit was an estimated length such that given the defined mass parameter of the sun (GM in au3/day2), a planet orbiting the sun under Newtonian gravity with a semi-major axis of one au and no other planets perturbing its orbit, would have an orbital period of exactly one year (365.25 days).
In 2012, a new definition (IAU 2012 Resolution B2) of the astronomical unit was adopted. The "au" is now a fixed number of meters and the GM value is estimated. This simplifies the ephemeris development process, aligns it with an updated IAU definition of solar system coordinate time (TDB) and recognizes that the mass parameter of the sun is changing with time.
What is the time scale used for the solar system ephemerides?
Coordinate time is the time used in the development of ephemerides for solar system objects. Under General Relativity, the rate at which actual clocks tick is called proper time. The rate of proper time depends on the location and motion of the clock, so there is no single proper time for the solar system as a whole. So for representing the motions of he solar system bodies using numerical integration, a time scale called 'coordinate time' is used, which is not the rate of any physical clock, but a parameter for which the equations of motion are simply expressed.
The integrated ephemerides for solar system bodies are stored as tables of positions and velocities as a function of coordinate time. In order to evaluate a measurement, such as the round-trip light time from Earth to Mars, or the direction to Saturn as seen from Earth, the proper times of the measurement must be converted to coordinate time before looking up the positions.
Currently the International Astronomical Union (IAU) has defined two coordinate times for the solar system and both are equally accurate. The coordinate time used for the JPL ephemerides, as the independent variable in the solar system, barycentric relativistic, equations of motion, is Barycentric Dynamical Time (TDB) or, in French, Temps Dynamique Barycentrique. This coordinate time is defined such that in the vicinity of the Earth the difference in coordinate time and international atomic time (TAI) is 32.184 seconds plus a small variation that is less than 3 milliseconds. TAI differs from Universal Coordinate Time (UTC) by an integer number of seconds (34 as of July 1, 2012), which changes only when leap seconds are added. UTC is the basis for civil time (e.g., Pacific Standard Time equals UTC - 8 hours).
The other solar system coordinate time defined by the IAU is Barycentric Coordinate Time (TCB, Temps-Coordonnée Barycentrigue), which differs from TDB by a defined offset and rate. TCB has the property that infinitely far from the Sun, where the curvature of space-time from the gravity of the Sun goes to zero, TCB and proper time tick at the same rate. This property makes some theoretical calculations have a simpler form, but causes a fairly large difference in rate between TCB and TAI near the Earth. TCB is not used in the development of JPL's ephemerides for solar system bodies.
What's the exact value of... <insert your favorite orbital element here>?
To have an exact value, a quantity must be either strictly constant, or else, exactly periodic.
The orbits of the planets are only approximately elliptical; their motions are only approximately periodic; not exactly. Therefore, it doesn't make much sense to ask questions about "exact" Keplerian (elliptical) elements.
A simple analogy would be to take a pencil and draw a free-hand circle on a piece of paper, going round-and-round a number of times. Then ask, "what is the EXACT radius of that circle?"
It is impossible to give an answer; the curve that you have drawn is not exactly a circle.
One may define an "osculating" radius, for example: the radius of curvature at any given point on the curve. However, this value is exact at that given point only. The value will change for a different place on the curve; or, if averaged over some portion of the curve; or, if averaged over some other portion of the curve.
Which result gives the "exact" answer? None; there is no "exact" radius for the curve.
It's a whole different situation with the JPL ephemerides. We do not use things such as periods, eccentricities, etc. Instead, we integrate the equations of motion in Cartesian coordinates (x,y,z), and we adjust the initial conditions in order to fit modern, highly accurate measurements of planetary positions. As a result, we are able to produce ephemerides which are far more accurate than those based upon elliptical elements.
In the analogy above, it could be possible to measure each point of the hand-drawn curve very accurately; however, one still could not give a unique value for the curve's radius.
What about planet X?
People used to think that the orbits of Uranus and Neptune could not be properly fit to the observations (measurements of their positions). Therefore, it was assumed that there was an additional planet out in the farther reaches of the solar system which was perturbing those planets' motions: i.e., Planet X. It is now known, however, that the orbits of Uranus and Neptune can be adjusted to the accuracy of the data if done properly (as in the reference below). Thus, no need for Planet X.
Over the past decade or so, a number of bodies have been found out past the orbit of Pluto. In fact, one of them is even bigger than Pluto; so, in some sense, it should be considered to be a planet. Is it "The Planet X"? No; neither it nor Pluto is close in enough or massive enough to significantly affect the orbits of Uranus or Neptune.
Standish,E.M.: 1993, "Planet X: No Dynamical Evidence in the Optical Observations", Astronomical Journal, 105, no.5, 2000-2006.




